Understanding Pipe Fitting Basics

Overview of Pipe Fitting Components

In the shadowy realm of infrastructure where steel and solder converge, understanding pipe fitting basics becomes an essential ritual. The components—elbows, tees, couplings, and flanges—are the silent guardians of fluid flow, each serving a purpose as vital as a heartbeat in a living organism. Their precise arrangement determines not only the efficiency of a system but also the longevity of the entire network. Pipe fitting equations become the arcane formulas guiding engineers through the labyrinth of angles, diameters, and pressure calculations.

These equations are the dark arts behind seamless connections, ensuring that every joint holds firm against the relentless tide of pressure and corrosion. The intricacies of fitting components demand a keen understanding of how they interact within the system. For example, the calculation of bend angles and their impact on flow resistance can be deciphered through specific pipe fitting equations, revealing the hidden symphony of fluid dynamics.

In the world of pipe fitting, mastery over these equations transforms chaos into order. Whether calculating the radius for a bend or determining the appropriate size for a coupling, each step is a dance with the unseen forces that govern the flow—an elegant balance of science and craftsmanship.

Common Types of Pipe Fittings

In the intricate dance of fluid mechanics, understanding pipe fitting basics is the heartbeat that sustains efficiency and durability. The common types of pipe fittings—elbows, tees, couplings, and flanges—are not mere connectors but vital cogs in a complex machinery of flow regulation. Each component’s geometry and material properties influence the system’s overall performance, making pipe fitting equations an essential tool for precise calculations.

These equations serve as the blueprint for engineers navigating the labyrinth of angles, diameters, and pressure parameters. For instance, calculating the radius of a bend or the optimal diameter for a coupling hinges on a mastery of pipe fitting equations, transforming theoretical mathematics into practical, seamless connections. When you consider how these components interact under pressure, the importance of accurate equations becomes undeniably clear.

To better grasp the scope, here’s a quick overview of common fittings and their typical applications:

1. Elbows—used to change the direction of flow, often requiring precise angle calculations.
2. Tees—facilitate branch connections, demanding accurate size matching through specific equations.
3. Couplings—join two pipes in a straight line, where diameter consistency is crucial.
4. Flanges—allow for easy assembly and disassembly, with pressure ratings tied to fitting equations.

Mastering the nuances of these fittings through the lens of pipe fitting equations unlocks a new level of craftsmanship—one where science and artistry converge to craft resilient, efficient piping systems across South Africa’s diverse industrial landscape.

Importance of Accurate Pipe Fitting Calculations

Every drop of water, every gust of wind, and every industrial process in South Africa relies on the seamless harmony of piping systems. Behind this harmony lies an often overlooked hero: the precision of pipe fitting equations. Accurate calculations are vital—without them, even the most durable pipes can falter under pressure or misalign, disrupting workflows and risking costly repairs.

Understanding the importance of pipe fitting equations is more than just mastering formulas. It’s about ensuring that each elbow, tee, or flange fits perfectly within the system’s unique demands. When these equations are applied correctly, they transform complex geometry into reliable, long-lasting connections. The result? A piping network that endures the test of time, even in challenging environments across South Africa’s diverse industries.

Fundamental Pipe Fitting Equations

Calculating Pipe Lengths and Diameters

In the world of piping systems, precision is everything—especially when it comes to pipe fitting equations. Accurate calculations of pipe lengths and diameters are the backbone of efficient plumbing, ensuring seamless flow and minimizing waste. Interestingly, even small deviations in these equations can lead to significant issues down the line, from pressure drops to structural vulnerabilities. This is why mastering fundamental pipe fitting equations is essential for professionals aiming for perfection in their projects.

When calculating pipe lengths, it’s crucial to consider factors such as bends, fittings, and elevation changes, all of which influence the overall measurement. For instance, a simple formula for pipe length may need to adapt based on the number of fittings involved or the pipe’s configuration. Here’s a quick overview of essential steps involved in these calculations:

• Assess the total distance between connection points.
• Include additional length for fittings, elbows, and other components.
• Adjust for elevation changes to ensure proper flow dynamics.

By applying these fundamental pipe fitting equations, installers can prevent costly mistakes and ensure that every inch of pipe fits perfectly within the intended system. It’s a meticulous process, but one that pays dividends in the longevity and efficiency of the piping infrastructure—something every professional in South Africa can appreciate!

Determining Flow Rate and Velocity

Flow rate and velocity are the unsung heroes of any piping system—without them, your water might as well be a stubborn mule refusing to move. When it comes to pipe fitting equations, understanding how to determine flow rate and velocity isn’t just academic; it’s the secret sauce to a well-oiled plumbing operation. Did you know that even a slight miscalculation can cause pressure surges or sluggish flow? That’s why wielding these equations with finesse is crucial for South African professionals who aspire to avoid plumbing nightmares.

Using fundamental pipe fitting equations, you can predict how fast water will race through your pipes and at what volume. For example, the basic formula involves cross-sectional area and flow velocity:

• Flow rate = Cross-sectional area × Velocity

This simple yet powerful equation allows installers to balance system design with real-world conditions. When calculating velocity, remember that it’s not just about speed; it impacts everything from water hammer to pipe wear and tear. Mastering these pipe fitting equations ensures your system runs smoothly, saving you from costly callbacks and frustrated clients—an achievement that South African plumbers can proudly toast to!

Pressure Loss and Head Loss Equations

Pressure loss and head loss equations are fundamental to understanding how fluid behaves within a piping system. When water encounters fittings, bends, or valves, it loses energy—this is where pressure loss equations come into play. These equations help predict how much pressure is dropped over a certain length of pipe, which is vital for maintaining optimal flow and avoiding system failures.

Head loss, expressed in meters or feet of fluid, quantifies energy reduction caused by friction and turbulence. It’s essential for designing systems that balance pressure and flow rate effectively. For practical purposes, many professionals rely on simplified formulas such as Darcy-Weisbach or Hazen-Williams, which are integral to the broader scope of pipe fitting equations. Here’s a quick overview:

1. Calculating pressure loss involves understanding pipe roughness, flow velocity, and pipe diameter.
2. Head loss equations incorporate factors like pipe material and fluid viscosity, ensuring precision in complex systems.

Mastering these pipe fitting equations ensures that South African plumbing systems operate efficiently—minimizing pressure drops and avoiding costly troubleshooting. Whether working on a small residential project or a large commercial installation, these equations are the backbone of reliable, durable piping networks.

Flow Continuity and Bernoulli’s Equation

In the intricate dance of fluid movement through piping systems, two fundamental pipe fitting equations reign supreme: the flow continuity equation and Bernoulli’s equation. These mathematical principles are the backbone of understanding how water and other fluids behave when navigating complex networks. Without them, predicting pressure variations and flow patterns becomes a game of chance—an outcome no professional wants in a high-stakes project.

The flow continuity equation asserts that, for an incompressible fluid, the volume flow rate remains constant within a closed loop. This means that if water speeds up in a narrower section of pipe, it must slow down elsewhere—an essential insight when designing fittings and bends. Bernoulli’s equation complements this by linking pressure, velocity, and elevation, revealing how energy transforms along the pipe’s course. By mastering these pipe fitting equations, engineers in South Africa can ensure systems operate smoothly, avoiding unexpected pressure drops that could spell disaster.

In practice, understanding these equations allows for precise adjustments in system design, especially when dealing with variable pipe diameters or complex layouts. Whether through the use of simplified or advanced formulas, the mastery of pipe fitting equations is vital—transforming theoretical knowledge into practical solutions that keep water flowing reliably and efficiently.

Specialized Pipe Fitting Formulas

Fitting Loss Coefficient (K)

In the intricate dance of fluid flow through pipes, the Fitting Loss Coefficient (K) emerges as a silent conductor, orchestrating the subtle nuances of pressure drops and energy dissipation. These specialized pipe fitting equations serve as vital tools, transforming complex geometries and turbulent interactions into comprehensible data. Understanding the fitting loss coefficient (K) unlocks the secrets behind the resistance caused by elbows, tees, valves, and other fittings—each with its own unique signature in the symphony of fluid dynamics.

Accurate calculation of K is crucial for engineers, especially in South Africa’s diverse infrastructural landscape, where precision can mean the difference between efficiency and disaster. The equations relate the velocity of flow to the energy loss, often expressed through the fundamental form:

• K = (2 * ΔP) / (ρ * v²)

Here, ΔP signifies the pressure loss, ρ the fluid density, and v the velocity. These pipe fitting equations are essential for designing systems that are both robust and economical, ensuring that every bend and branch contributes harmoniously to the overall performance of the pipeline. When properly applied, they illuminate pathways to optimal flow, safeguarding against unexpected failures and inefficiencies.

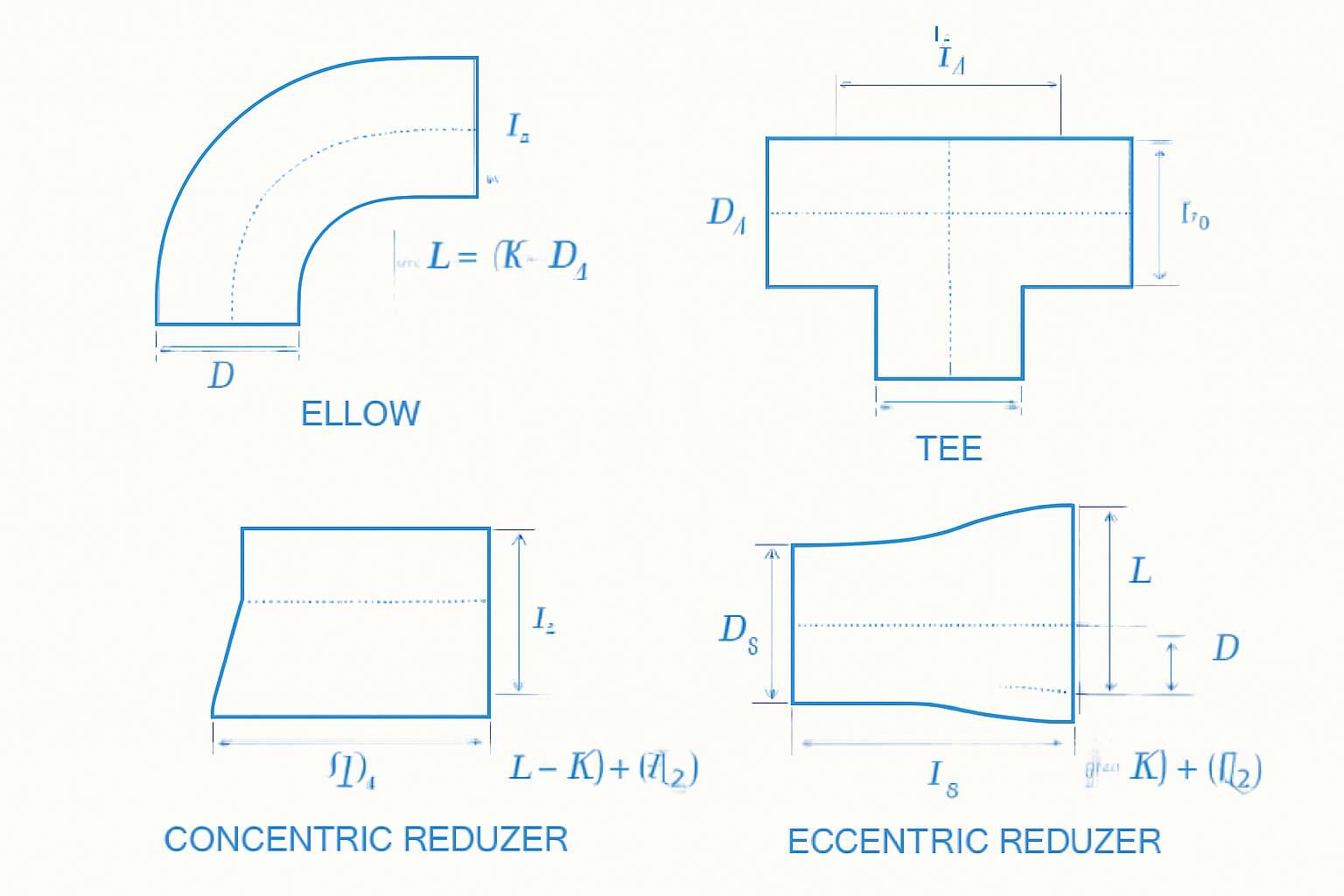
Elbow and Bend Equations

In the realm of fluid dynamics, understanding the nuances of pipe fitting equations can elevate a project from mere functionality to a masterpiece of engineering precision. Among these, elbow and bend equations stand out as vital tools, revealing how curvature influences flow resistance. When water or other fluids navigate a bend, the smoothness of the turn and the radius of curvature significantly impact pressure loss. These variables are the foundation of specialized pipe fitting equations, which translate complex geometrical interactions into manageable data.

For elbows and bends, the flow resistance is often expressed through the fitting loss coefficient (K), which varies depending on the radius-to-diameter ratio. Engineers rely on the following simplified relation:

1. K = (2 * ΔP) / (ρ * v²)

This equation encapsulates the energy dissipation caused by curvature. To refine calculations, different types of bends—such as long-radius or short-radius—demand specific coefficients derived from empirical data. Recognizing these distinctions ensures that every twist in the pipeline contributes to efficiency rather than unwarranted pressure loss, a crucial consideration for South Africa’s diverse infrastructural demands.

Ultimately, mastery of pipe fitting equations for elbows and bends enables engineers to craft systems where fluid flow is both seamless and resilient. Each curve, each bend, tells a story—one where physics and precision dance harmoniously in the pursuit of engineering excellence.

Reducer and Expander Calculations

Within the intricate tapestry of fluid mechanics, specialized pipe fitting equations serve as the silent architects shaping the efficiency and resilience of piping systems. Among these, reducer and expander calculations stand as pivotal elements—transforming complex geometrical alterations into precise, manageable data points. These equations are not mere numbers but the language through which engineers articulate the subtle dance of flow dynamics as it navigates through varying diameters.

Reducers and expanders play a crucial role in optimizing flow and minimizing turbulence. Their calculations often involve intricate formulas that account for the transition’s smoothness, ensuring minimal pressure loss and energy dissipation. For example, the flow behavior through a reducer can be described by specialized pipe fitting equations that consider the change in cross-sectional area, velocity, and pressure.

To accurately determine the dimensions and flow characteristics, engineers frequently use detailed formulas such as:

• Velocity and pressure adjustments based on diameter ratios
• Empirical coefficients derived from extensive testing
• Transition smoothness influencing flow resistance

The precision embedded in these pipe fitting equations ensures that every expansion and contraction in the pipeline aligns seamlessly with the overarching goal of efficiency. It’s a delicate interplay—each calculation a testament to the engineering mastery required to shape resilient, high-performance systems. In South Africa’s diverse infrastructural landscape, these formulas are more than academic exercises; they are vital tools in crafting sustainable, optimized pipelines that stand the test of time.

T-Piece and Cross Fitting Equations

In the realm of advanced pipe fitting equations, T-piece and cross fitting calculations serve as the labyrinthine backbone of complex piping systems. These fittings aren’t just simple connectors; they are pivotal junctions that demand meticulous mathematical precision to ensure seamless flow and structural integrity. The equations governing T-pieces and cross fittings delve into the nuances of flow distribution, pressure balancing, and velocity adjustments, transforming raw data into elegant solutions.

For T-pieces, the equations often involve balancing the flow rates through each branch, considering the impact of junction angles and the velocity of fluid. Cross fittings, on the other hand, require a more intricate approach—accounting for simultaneous flow paths and potential turbulence. To navigate this complexity, engineers frequently rely on specialized pipe fitting equations that incorporate empirical coefficients and flow resistance factors, ensuring each connection maintains optimal performance. In South Africa’s diverse infrastructural landscape, mastering these formulas is essential for crafting pipelines that are both resilient and efficient.

Applications of Pipe Fitting Equations in Industry

HVAC System Design

In the intricate dance of HVAC system design, the mastery of pipe fitting equations transforms a chaotic tangle of pipes into a symphony of efficiency. Each calculation acts as a guiding compass, ensuring air flows seamlessly through labyrinthine ductwork while minimizing energy loss. These equations are not mere numbers; they are the silent architects shaping the harmony between performance and sustainability.

When engineers harness the power of pipe fitting equations, they unlock a realm of precision that elevates system reliability. From calculating pressure drops to optimizing flow rates, these formulas serve as the backbone of resilient HVAC infrastructures. In the South African industrial landscape, where climate variability demands adaptability, mastering pipe fitting equations becomes a vital craft—an art form that blends scientific rigor with inventive problem-solving.

Understanding the nuanced interplay of pipe fitting equations allows professionals to anticipate challenges before they arise. Whether designing for maximum airflow or ensuring energy efficiency, these calculations forge the path toward innovation and sustainability in the field of HVAC system design. It’s an orchestration of science and ingenuity, powered by the steadfast logic of pipe fitting equations!

Water Supply and Drainage Calculations

In South Africa’s expanding industrial landscape, the application of pipe fitting equations extends beyond HVAC systems into vital water supply and drainage systems. Accurate calculations are essential to ensure that water flows efficiently and that drainage performs reliably, even amidst the country’s diverse climate challenges. These equations help engineers determine optimal pipe diameters, flow rates, and pressure losses, preventing costly errors and system failures.

For water supply networks, understanding the interplay of pipe fitting equations can mean the difference between a steady flow and persistent bottlenecks. Similarly, in drainage design, these formulas facilitate the creation of systems that handle varying load capacities while minimizing blockages. When applied correctly, pipe fitting equations enable professionals to balance hydraulic performance with economic efficiency, ensuring sustainable infrastructure development.

Oil and Gas Pipeline Engineering

In South Africa’s dynamic oil and gas industry, the precision of pipe fitting equations can make or break a pipeline project. These equations are the backbone of designing systems that withstand the country’s complex geological and environmental challenges. When engineers accurately apply pipe fitting equations, they can predict pressure drops, optimize flow rates, and select the right pipe diameters—ensuring safety and efficiency at every stage.

Consider the critical role of fitting loss coefficients and bend equations in reducing turbulence and minimizing energy consumption. For example, calculating the pressure loss across elbows and reducers with pipe fitting equations helps prevent costly overdesigns or unexpected failures. This meticulous approach supports the sustainable development of infrastructure in regions where resource management is vital.

In the realm of pipeline engineering, the strategic application of pipe fitting equations ensures that flow integrity is maintained under varying load conditions. It’s not just about technical accuracy; it’s about creating resilient systems capable of adapting to South Africa’s diverse operational demands. The nuanced understanding of these equations transforms theoretical calculations into practical solutions that safeguard both personnel and investments.

Industrial Manufacturing Processes

In the shadowy corridors of industrial manufacturing, where steel and fire intertwine, pipe fitting equations serve as the silent guardians of integrity. These equations breathe life into the seemingly cold metal veins that weave through factories and processing plants, ensuring that every flow is precise and unyielding. When wielded with mastery, pipe fitting equations become the alchemy that transforms raw materials into seamless systems capable of withstanding the relentless pressures of modern industry.

Within the labyrinth of industrial processes, the application of pipe fitting equations is critical. They allow engineers to anticipate pressure drops, optimize flow rates, and select the perfect pipe diameters—an orchestration that prevents catastrophic failures and costly downtimes. Whether calculating the flow of corrosive chemicals or steam in complex manufacturing setups, these equations form the backbone of resilient infrastructure.

In this realm of shadows and precision, understanding the nuances of fitting loss coefficients and bend equations is essential. They help tame turbulence, reduce energy consumption, and maintain the integrity of the entire system. When every calculation aligns perfectly, the industrial symphony plays on—silent but unstoppable—guided by the careful application of pipe fitting equations.

Tools and Resources for Pipe Fitting Calculations

Pipe Fitting Calculators

When it comes to mastering pipe fitting equations, having the right tools and resources can transform a daunting task into a seamless process. Advanced pipe fitting calculators are invaluable in ensuring precision, especially when working within complex systems. These digital tools automate the intricate calculations, reducing errors and saving precious time on-site. Whether you’re calculating flow rates or determining pressure drops, a reliable calculator can be your secret weapon in achieving perfect fits every time.

For professionals in South Africa, accessing high-quality resources is crucial. Many online platforms offer comprehensive pipe fitting equations calculators tailored specifically for local standards and conditions. These tools often include features such as automatic conversion of units and real-time adjustments, which are essential when dealing with diverse piping materials and configurations. Here’s a quick overview of what to look for:

1. Intuitive interface that simplifies complex calculations
2. Built-in databases of pipe sizes and fittings
3. Compatibility with mobile devices for on-the-go access

With these tools at your fingertips, tackling pipe fitting equations becomes less of a chore and more of an art, ensuring your projects are both efficient and accurate. In the world of piping systems, having the right resources can make all the difference between success and costly mistakes.

Engineering Software Solutions

In the realm of pipe fitting equations, accessing reliable engineering software solutions can elevate a project’s precision and efficiency. Modern tools are designed to streamline complex calculations, transforming what once took hours into moments of clarity. These software solutions often feature intuitive interfaces and robust databases, making it easier for professionals to input data and receive accurate results swiftly.

Furthermore, many platforms are compatible with mobile devices, allowing engineers and technicians to perform critical calculations right on-site. This flexibility is invaluable in the field, where quick decision-making can save time and resources. For example, some advanced pipe fitting calculators accommodate local standards and material properties relevant to South Africa, ensuring compliance and optimal performance.

Choosing the right resources for pipe fitting equations is not just about convenience but about safeguarding the integrity of your entire system. Whether through dedicated software solutions or online calculators, these tools serve as essential companions in the quest for perfect pipe joins and seamless flow management.

Standards and Code References

In the intricate dance of pipe fitting equations, having the right tools and resources is like wielding a master key to flawless system design. The labyrinth of standards and code references can seem daunting—unless you have a trusted map. Thankfully, industry standards such as SANS (South African National Standards) and international codes like ASME B31.3 are your best friends, ensuring every calculation aligns with local regulations and safety protocols.

For those who prefer digital companions, a wealth of online resources and dedicated engineering software solutions can expedite your calculations while maintaining accuracy. These platforms often come with built-in compliance checks and material property databases tailored for South African industries, from water treatment to oil pipelines. To streamline your workflow, consider integrating these tools with your project management systems. After all, efficiency isn’t just about speed; it’s about precision.

When diving into pipe fitting equations, don’t forget the importance of referencing authoritative standards. They serve as the backbone for validation and safety, especially when working on critical infrastructure. Whether you’re calculating bend radii, fitting loss coefficients, or flow velocities, these standards ensure your results are not only mathematically sound but also compliant with local regulations.

• South African National Standards (SANS)
• ASME B31.3 Process Piping Code
• ISO 9001 Quality Management Systems

By leveraging both cutting-edge software and rigorous standards, professionals in South Africa can confidently navigate the complex realm of pipe fitting equations. It’s this blend of technology and regulation that transforms a puzzling array of numbers into a seamless, reliable piping system—proof that good tools make good engineers. After all, a miscalculation isn’t just an error; it’s a potential catastrophe waiting to happen.

Educational Resources and Tutorials

Mastering pipe fitting equations requires more than just raw numbers—it’s about harnessing the right tools and resources that turn complex calculations into precise, reliable results. Digital solutions, such as specialized engineering software, have revolutionized the way professionals approach these equations. With features like built-in compliance checks and extensive material databases, these tools streamline processes, reducing errors and saving valuable time. For projects in South Africa, choosing software tailored to local standards and regulations enhances accuracy and safety.

Educational resources and tutorials also play a pivotal role in sharpening skills. Online platforms offer comprehensive guides, step-by-step walkthroughs, and interactive modules that demystify challenging aspects of pipe fitting equations. Engaging with these materials deepens understanding and ensures adherence to industry standards like SANS and ASME B31.3. Whether you’re calculating bend radii or flow velocities, the right educational tools empower you to navigate the intricacies of pipe fitting equations confidently.